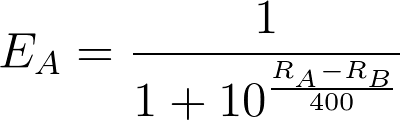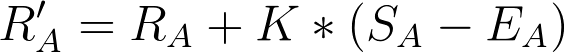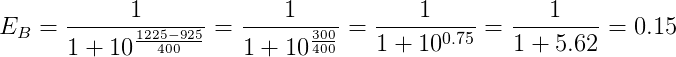Ranked Matchmaking

This type of matchmaking is used in tournaments and any other competition that has to select opponents of similar skill levels.

Ranked matchmaking is based on the Elo rating system.

A tournament participant can see their rank at the portal at https://tss.warthunder.com/ by logging into their account and clicking “Rating” in the menu. Rating is calculated individually for each game mode and difficulty level. A rating is given if the player has completed at least one battle in a relevant tournament.

Rating Generation

Each player starts with a rating of 1,000 points. Later, the rating is calculated based on tournament battle results, using this formula:

Where

• Е_А is the expected value (from 0 to 1) for the number of points Player A will earn in a game with Player B
• R_A is Player A’s rating
• R_B is Player B’s rating

The rating points for Player A are calculated based on the outcome of the match:

Where

• R’_A is Player A’s rating after the match
• R_A is Player A’s current rating
• S_A is the number of points gained as a result of the match (1 for a victory, 0.5 for a tie, and 0 for a loss)
• K is a fixed coefficient with a value of 10

Team ratings are calculated as the average rating of all players registered in the team.

An example of formula calculations

Only victories and defeats in tournament battles or other competitions affect player ratings in War Thunder. Actions taken during the battle have no effect on ratings.

Let’s say that Player A has a current rating of 1225 points and Player B has a rating of 925. 

The expected result for Player A would be:

Player B’s expected result would be:

If Player A wins the match, we get these results:

R’_A = 1225 + 10 * (1 - 0.85) = 1225 + 1.5 = 1226.5

R’_B = 925 + 10 * (0 - 0.15) = 925 - 1.5 = 923.5 

If Player B wins, the result will be:

R’_A = 1225 + 10 * (0 - 0.85) = 1225 - 8.5 = 1216.5

R’_B = 925 +10 * (1 - 0.15) = 925 + 8.5 = 933.5 

So, an experienced player with a high rating gets a much smaller gain for winning against a weak player than a weaker player who defeats a strong opponent.